Relations
Definition
A triple , where are sets and is called a binary relation. The set is called the domain, the set is called the codomain and the set is called the graph of the relation . If , then the relation is called homogeneous If , then we sometimes write and we say that a has the relation r to b or a and b are related with respect to the relation r.
Definition
Let be a relation and let . Then the set is called the relation class of X with respect to r. If , then we denote
Notice that
If A,B are finite sets, then may be represented by a diagram consisting of two sets with elements and connecting arrows. For instance, let where , and
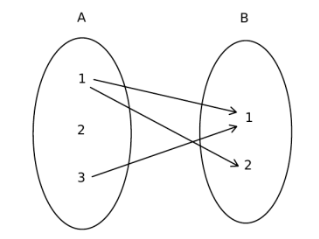 Figure: Diagram of a relation.
Also note that
Figure: Diagram of a relation.
Also note that
Examples of relations
a. Let be the set of all children and let be the set of all parents. Then we may define the relation , where
b. The triple , where
is a homogeneous relation, called the inequality relation on . We have
c. There are several examples from Number Theory, such as divisibility on or on , and Geometry, such as parallelism of lines, perpendicularity of lines, congruence of triangles, similarity of triangles
d. Let and be two sets. Then the triples
are relations, called the void relation and the universal relation respectively.
e. Let be a set. Then the triple , where is called the equality relation on .
f. Every function called is a relation. Indeed, a function is determined by its domain , its codomain and its graph
Then the triple is a relation.
g. Every directed graph is a relation.
For instance the directed graph
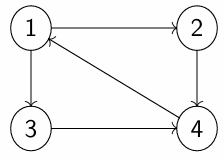 may be seen as a relation , where and
may be seen as a relation , where and
Functions
Definition
A relation is called a function if that is, the relation class with respect to r of every consist of exactly one element.
In what follows, if is a function, we will mainly use the classical notation for a function, namely or sometimes . The unique element of the set will be denoted by . Then we have
Related notions
From relations we get the following notions.
Definition
Let be a function. Then A is called the domain, is called the codomain and is called the graph of the function f.
Examples of functions and relations
a. b.
Equivalence relations
Recall that a relation is called homogeneous if .
Definition
A homogeneous relation on is called :
- reflexive (r) if:
- transitive (t) if:
- symmetric (s) if:
A homogeneous relation is called an equivalence relation if has the properties (r), (t), (s).
Examples of equivalence relations
Partitions
Definition
Let be a non-empty set. Then a family of non-empty subsets of is called a partition of if:
- The family covers , that is,
- The ‘s are pairwise disjoint, that is,
Examples of partitions
(a) Let and . Then is a partition of . (b) Let be a set. Then and are partitions of . (c) Let be the set of even integers and the set of odd integers. Then is a partition of . (d) Consider the intervals for every . then the family is a partition of .